Kamis, 11 September 2014
Jumat, 21 Maret 2014
ASAL MULA TRIGONOMETRI
ASAL MULA TRIGONOMETRI
1. Pengertian
Trigonometri
Trigonometri berasal daro bahasa
Yunani yaitu tri artinya tiga,gonomon artinya sudut
dan metria yg artinya ukuran jadi. Jadi, trigonometri adlh pengukuran
sudut segitiga.
Menurut Edward J. Byng bahwa
trigonometri adlh ciptaan orang arab. Oleh karena itu, banyak kata-kata dalam
trigonometri yg menggunakan istilah dari Arab.
2. Awal
Kemunculan Trigonometri
Walaupun pd mulanya trigonometri
dikaji sebagai cabang astronomi tetapi akhirnya trigonometri berdiri sendiri
sebagai sebuah disiplin ilmu. Perkembangan awal trogonometri terbukti
digerakkan disebabkan keperluan penyelesaian masalah astronomi. Kemunculan
trigonometri merupakan proses yg perlahan. Jika dibandingkan dg cabang
matematika lain, trigonometri berkembambang disebabkan hubungan antara
pendidikan matematika terapan dg keperluan sains dalam bidang astronomi.
Hubungan ini dianggap saling berkait, tetapu tersembunyi sehingga zaman
Renaissans trigonometri dijadikan sebagai topik tambahan dalam astronomi.
3. Perkembangan
dan Tokoh-Tokoh Trigonometri
Trigonometri sebagai alat utama
astronomi telah menjadi bidang kajian yg sangat diminati oleh ahli-ahli
matematika islam sehingga trigonometri dapat berdiri sendiri sebagai sebuah
disiplin ilmu. Orang islam adlh orang yg pertama kali
menekankan pengkajian prinsip-prinsip cahaya. Ia adlh al-Haitham, yg telah
menulis risalah-risalah penting tentang topik. Al-Haitham membina bentuk awal
prinsip-prinsip cahaya yg akhirnya menjadi hukum snell tentang pembiasan
cahaya. Prinsip oprik al-Haitham memberu sesuatu insipirasi supaya perhatian
terhadap astronomi dan trigonometri lebih diutamakan. Berikut ini beberapa nma
tokoh dalam trigonometri :
Al-Khawarizmi
Al-Khawarizmi adlh seorang tokoh
matematika besar yg [ernah dilahirkan islam dan disumbangkan pd peradaban
dunia. Mungkin tak seratus tahun sekali akan lahir kedunia orang-orang seperti
beliau. Al-Khawarizmi selain terkenal dg teori algoritmanya, beliau juga
membangun teori-teori matematika lain. dalam bidang trigonometri beliau
menemukan pemakaian sin, cos, tangent dan secan.
Al-Battani
Nma lengkap al-Battani adlh Mohammad
Ibn Jabir Ibn Sinan Abu Abdullah Al-Battani, dilahirkan di Battan Mesopotamia pd
tahun 850 M dan meninggal meninggal dunia di Damsyik pd tahun 929 M. Beliau adlh
putra raja Arab, juga gubernur Syria yg dianggap sebagai ahli astronomi dan
ahli matematika islam yg terkemuka. Al-Battani yg bertanggung jawab
memperkenalkan konsep-konsep modern, perkembangan fungsi-fungsi dan identity
trigonometri. Beliau biasanya menggunakan formula sinus dg lebih jelas
dibandingkan penjelasan dari orang Yunani.
Abu al-Wafa
Nma lengkapnya adlh Abu al-Wafa
Muhammad Ibn Muhammad Ibn Yaya Ibn Ismail al-Buzjani lahir di Buzjan, Nishapur,
Iraq tahun 940 M. sejak kecil, kecerdasannya sudah mulai nampak dan hal
tersebut ditunjang dg minatnya yg besar di bidang ilmu alam.
Setelah berhasil menyelesaikan
pendidikan dasar dan menengahnya, Abu al-Wafa memutuskan untuk meneruskan ke
jenjang yg lebih tinggi di Baghdad pd tahun 959 M. Berkat bimbingan sejumlah
ilmuwan terkemuka masa itu, tak berapa lama ia menjelma menjadi seorang pemuda yg
berotak cemerlang. Dia pun lantas banyak membantu para ilmuwan serta
secara pribadi mengembangkan teori terutama dalam bidang trigonometri.
Konstruksi bangunan trigonometri versi abu al-Wafa diakui sengat besar
manfaatnya. Beliau mengembangkan metode baru tentang konstruksi segi empat
serta perbaikan nilai sinus 30 dg memakai delapan decimal.
Banyak buku dan karya ilmiah telah
dihasilkannya dan mencakup banyak bidang ilmu. Namun, tak banyak karyanya yg
tertinggal hingga saat ini. Sejumlah karyanya hilang, sedang yg masih ada sudah
dimodifikasi. Abu al-Wafa juga banyak menuangkan karya tulisnya di jurnal
ilmiah Euclid, Diophantus dan al-Khawarizmi, tetapi saygnya banyak yg telah
hilang. Karena konstribusinya yg besar terhadap bidang trigonometri,
beliau dijuluki sebagai peletak dasar ilmu trigonomteri.
Ibn al-Shatir
Nma lengkapnya adlh ‘Ala al-Din Ali
Ibn Ibrahim Ibn al-Muwaqit, lahir pd tahun 1306 M dan meninggal tahun 1375.
karyanya tertuang dalam rasad ibn shatir (pemerhati ibn shatir).
4. Aplikasi
Trigonometri
Jauh sebelum astronom muslim
mengembangkan metode pengamatan dan teoritisnya yg maju, mereka sudah memiliki
keahlian dalam menerapkan pengetahuan astronomi untuk memenuhi kebutuhan dasar
dalam ibadah. Praktek agama islam selalu memerlukan penentuan waktu dan
tempat, apakah dalam kaitan dg shalat atau untuk menentukam awal bulan dan hari
libur dalam kalender hijriah muslim
Shalat harus terarah dan waktunya
juga tertentu. Seluruh kaum muslimin shalat menghadap mekag kota kuno yg
menjadi tempat bangunan suci umat islam, yakni ka’bah. Kebutuhan administrasi
dan komunikasi pd awal-awal ekspansi islam menghasilkan kebutuhan kalender baru
yg islami. Sehingga khalifah yg berkuasa pd abad ke-7 membuat suatu sistem baru
yg berbeda dg kalender Gregorian dan Julian didasarkan pd siklus bulan
(kabisat) bukannya siklus matahari. Kalender baru ini berawal pd hari pertama
tahun hijrah (622 M), kepindahan nabi Muhammad dari Mekkah ke Madinah. Tanggal
ini yg diperkirakan terjadi pd akhir September, menandai awal tahun satu dalam
kalender islam. Fakta bahwa kalender tersebut didasarkan pd tahun kabisat
membuat prosedur konversi antara kalender islam dan kalender Gregorian menjadi rumit.
Seluruh hari libur dan hari raya muslim, dan juga ramadhan sebagai bulan untuk
berpuasa dijadwalkan pd tahun kabisat. Maka penampakan bulan sabit yg pertama pd
bulan yg baru merupakan momen penting bagi seluruh ibadah muslim. Alat
astronomi yg paling spektakuler adlh astrolabus, merupakan instrument
perhitungan yg penting pd abad pertengahan dan awal-awal renaissans. Selain
menentukan waktu shalat dan arah mekkah, astrolabus sebagai penentu waktu dan
perputaran tahunan benda-benda langit, pengukuran diatas bumi dan informasi
astrologi.
Selasa, 15 Oktober 2013
FPB dan KPK
Menentukan FPB dan KPK
1. Faktor Prima
Faktor prima suatu bilangan-bilangan prima yang dapat membagi habis bilangan tersebut.
Faktor dari 24 adalah 1, 2, 4, 6, 8, 12, dan 24
2 dan 3 merupakan bilangan prima yang dapat membagi habis 24.
Jadi, faktor prima dari 24 adalah 2 dan 3
- Bilangan prima adalah bilangan yang tepat mempunyai dua faktor atau bilangan yang hanya dapat dibagi dengan satu dan bilangan itu sendiri
Contoh : 2, 3, 5, 7, 11, 13, 17, …
2. Faktorisasi Prima
Faktorisasi prima adalah perkalian semua faktor-faktor prima dari suatu bilangan.
Contoh:
faktorisasi prima dari 48 = 2 x 2 x 2 x 2 x 3 = 24 x 3
faktorisasi prima dari 100 = 2 x 2 x 5 x 5 = 22 x 52
3. Kelipatan Persekutuan Terkecil (KPK)
Kelipatan persekutuan terkecil dari dua bilangan adalah bilangan terkecil yang habis dibagi kedua bilangan tersebut.
Cara menentukan KPK adalah dengan mengalikan semua faktor prima dari bilangan-bilangan tersebut. Jika ada faktor prima yang sama, diambil faktor prima memiliki pangkat terbesar.
Contoh:
Tentukan KPK dari 88 dan 68
Jawab:
Faktorisasi prima dari 88 = 2 x 2 x 2 x 11 = 23 x 11
Faktorisasi prima dari 68 = 2 x 2 x 17 = 22 x 17
KPK dari 88 dan 68 = 23 x 11 x 17 = 1.496
Jadi, KPK dari 88 dan 68 adalah 1.496
4. Faktor Persekutuan Terbesar (FPB)
Faktor persekutuan terbesar dari dua bilangan adalah bilangan terbesar yang habis membagi kedua bilangan tersebut.
Cara menentukan FPB adalah dengan mengalikan pangkat terkecil dari bilangan- bilangan tersebut dan diambil hanya faktor yang sama.
Contoh:
Tentukan FPB dari 88 dan 68!
Jawab:
Faktorisasi prima dari 88 = 2 x 2 x 2 x 11 = 23 x 11
Faktorisasi prima dari 68 = 2 x 2 x 17 = 22 x 17
FPB dari 88 dan 68 = 22 = 2 x 2 = 4
Jadi, FPB dari 88 dan 68 adalah 4
Sabtu, 05 Oktober 2013
Persamaan Linier Satu Variabel (PLSV)
Persamaan Linier Satu Variabel (PLSV)
Persamaan linier satu variable adalah persamaan yang hanya menggunakan satu variable saja (hanya satu variable)
1. Kalimat terbuka
Kalimat terbuka adalah kalimat matematika yang belum jelas benar dan salahnya.
Kalimat pernyataan adalah kalimat yang mempunyai nilai benar atau salah
Contoh kalimat benar
Jumlah dari enam dan dua adalah delapan
Enam dikurangi dua adalah empat
Contoh kalimat salah
Tujuh habis dibagi tiga
Persegi memiliki satu sisi
Jadi
Kalimat benar adalah kalimat yang pernyataannya memiliki nilai benar
Kalimat salah adalah kalimat yang pernyataannya memiliki nilai salah
2. Persamaan linier Satu Variabel
Pesamaan linier satu variable adalah persamaan yang hanya menggunakan satu variable saja (hanya satu variable)
Bentuk umum
ax + b = c 0, x = perubah
Persamaan linier dapat diselesaikan dengan cara
a. Menambah, mengurangi, membagi atau mengali dengan bilangan yang sama
b. Setiap pemindahan ruas, dari kirikekanan atau sebaliknya dapat diikuti perubahan tanda dari positif ke negatif atau sebaliknya.
Contoh
1. 4x -12 = 20
Jawab
4x -12 = 20
4x = 20 + 12
4x = 32
x= 8
2. 5x -20 = 10
Jawab
5x – 20 = 10
5x = 20 + 10
5x = 30
x = 6
Penerapan Untuk Persamaan Linier dalam Sehari-hari
Contoh
Jumlah siswa kelas 2 adalah 40 siswa. Jika jumlah siswa laki-laki sebanyak 12 siswa, berapa jumlah siswa perempuan.
Jawab
a + 12 = 40
a = 40 -12
a = 28
Persamaan linier satu variable adalah persamaan yang hanya menggunakan satu variable saja (hanya satu variable)
1. Kalimat terbuka
Kalimat terbuka adalah kalimat matematika yang belum jelas benar dan salahnya.
Kalimat pernyataan adalah kalimat yang mempunyai nilai benar atau salah
Contoh kalimat benar
Jumlah dari enam dan dua adalah delapan
Enam dikurangi dua adalah empat
Contoh kalimat salah
Tujuh habis dibagi tiga
Persegi memiliki satu sisi
Jadi
Kalimat benar adalah kalimat yang pernyataannya memiliki nilai benar
Kalimat salah adalah kalimat yang pernyataannya memiliki nilai salah
2. Persamaan linier Satu Variabel
Pesamaan linier satu variable adalah persamaan yang hanya menggunakan satu variable saja (hanya satu variable)
Bentuk umum
ax + b = c 0, x = perubah
Persamaan linier dapat diselesaikan dengan cara
a. Menambah, mengurangi, membagi atau mengali dengan bilangan yang sama
b. Setiap pemindahan ruas, dari kirikekanan atau sebaliknya dapat diikuti perubahan tanda dari positif ke negatif atau sebaliknya.
Contoh
1. 4x -12 = 20
Jawab
4x -12 = 20
4x = 20 + 12
4x = 32
x= 8
2. 5x -20 = 10
Jawab
5x – 20 = 10
5x = 20 + 10
5x = 30
x = 6
Penerapan Untuk Persamaan Linier dalam Sehari-hari
Contoh
Jumlah siswa kelas 2 adalah 40 siswa. Jika jumlah siswa laki-laki sebanyak 12 siswa, berapa jumlah siswa perempuan.
Jawab
a + 12 = 40
a = 40 -12
a = 28
Barisan dan Deret Aritmatika
BARISAN ARITMATIKA
Barisan bilangan adalah urutan dari bilangan yang dibuat berdasarkan aturan tertentu. Sedangkan untuk barisan aritmatika adalah sebuah barisan bilangan dimana setiap pasangan suku-suku yang berurutan memiliki selisih yang sama. contoh : 4,6,8,10,....
Selisih bilangan pada barisan aritmatika disebut beda yang biasa disimbolkan dengan huruf b, untuk contoh diatas memiliki nilai beda 2. Dan bilangan yang menyusun suatu barisan disebut suku, dimana suku ke n dari suatu barisan disimbolkan dengan Un sehingga untuk suku ke 5 dari suatu barisan biasa disebut dengan U5. Khusus untuk suku pertama dari suatu barisan biasa disimbolkan dengan huruf a.
Jadi bentuk umum untuk suatu barisan aritmatika yaitu U1,U2,U3, … ,Un-1 atau a, a+b, a+2b, … , a+(n-1)b
Menentukan Rumus Suku ke-n suatu barisan
Pasangan suku-suku berurutan dari suatu barisan aritmatika mempunyai beda yang sama, maka
U2 = a + b
U3 = U2 + b = (a + b) + b = a + 2b
U4 = U3 + b = (a + 2b) + b = a + 3b
U5 = U4 + b = (a + 3b) + b = a + 4b
Berdasarkan pola tersebut, dapatkah sobat menentukan suku ke-7, suku ke-26 hingga suku ke-90? Dengan menggunakan pola diatas kita dapat mengetahui dengan mudah suku-suku tersebut.
U7 = a + 6b
U26 = a + 25b
U90 = a + 89b
Sehingga berdasarkan runtutan penjelasan diatas untuk suku ke-n dapat kita peroleh menggunakan rumus :
Un = a + (n – 1)b, untuk n bilangan asli
DERET ARITMATIKA
Yang dimaksud dengan deret aritmatika adalah penjumlahan dari semua anggota barisan aritmatika secara berurutan. Contoh dari deret aritmatika yaitu 7 + 10 + 13 + 16 + 19 + …
Misalnya kita ambil n suku pertama, jika kita ingin menentukan hasil dari deret aritmatika sebagai contoh untuk 5 suku pertama dari contoh deret diatas. Bagaimana caranya?
7 + 10 + 13 + 16 + 19 = 65
Nah untuk 5 suku pertama, masih mungkin kita menghitung manual seperti diatas. Seandainya kita akan menentukan jumlah dari 100 suku pertama, apakah masih mungkin kita menghitung manual seperti itu. Walaupun bisa tetapi pastinya akan memakan waktu yang cukup lama. Nah kali ini akan kita tunjukkan cara menentukannya, sebagai contohnya untuk mennetukan jumlah 5 suku pertama dari contoh diatas.
Misalkan S5=7 + 10 + 13 + 16 + 19, sehingga
Deret Aritmetika
Walaupun dengan cara yang berbeda tetapi menunjukkan hasil yang sama yaitu 65. Perhatikan bahwa S5 tersebut dapat dicari dengan mengalikan hasil penjumlahan suku pertama dan suku ke-5, dengan banyaknya suku pada barisan, kemudian dibagi dengan 2. Analogi dengan hasil ini, jumlah n suku pertama dari suatu barisan dapat dicari dengan rumus berikut:
Sn = (a + Un) × n : 2
Dikarenakan Un = a + (n – 1)b, sehingga rumus di atas menjadi
Sn = (2a + (n – 1)b) × n : 2
DERET ARITMATIKA
Sisipan pada deret aritmatika yaitu menambahkan beberapa buah bilangan diantara dua suku yang berurutan pada suatu deret aritmatika sehingga diperoleh deret aritmatika yang baru. Sebagai contoh :
Deret mula-mula = 4 + 13 + 22 + 31 +……
Setelah disisipi = 4 + 7 + 10 + 13 + 16 + 19 + 22 + 25 + 28 + 31 +……
Untuk beda dari deret baru ini biasanya dinyatakan dengan b1, dapat ditentukan dengan rumus berikut :
b1 = b/(k+1)
b1 = beda deret baru
b = beda deret mula-mula
k = banyak bilangan yang disisipkan
Barisan dan Deret Aritmatika tergolong materi yang mudah dipahami, sehingga diharapkan hanya dengan membaca artikel ini sobat semua telah mengerti tentang materi ini. Walaupun demikian, latihan soal harus tetap berjalan agar kemampuan kita selalu terasah. Materi sebelumnya yang dapat dipelajari juga yaitu Frekuensi Harapan dan Peluang Komplemen Suatu Kejadian dari sub bab peluang.
Barisan bilangan adalah urutan dari bilangan yang dibuat berdasarkan aturan tertentu. Sedangkan untuk barisan aritmatika adalah sebuah barisan bilangan dimana setiap pasangan suku-suku yang berurutan memiliki selisih yang sama. contoh : 4,6,8,10,....
Selisih bilangan pada barisan aritmatika disebut beda yang biasa disimbolkan dengan huruf b, untuk contoh diatas memiliki nilai beda 2. Dan bilangan yang menyusun suatu barisan disebut suku, dimana suku ke n dari suatu barisan disimbolkan dengan Un sehingga untuk suku ke 5 dari suatu barisan biasa disebut dengan U5. Khusus untuk suku pertama dari suatu barisan biasa disimbolkan dengan huruf a.
Jadi bentuk umum untuk suatu barisan aritmatika yaitu U1,U2,U3, … ,Un-1 atau a, a+b, a+2b, … , a+(n-1)b
Menentukan Rumus Suku ke-n suatu barisan
Pasangan suku-suku berurutan dari suatu barisan aritmatika mempunyai beda yang sama, maka
U2 = a + b
U3 = U2 + b = (a + b) + b = a + 2b
U4 = U3 + b = (a + 2b) + b = a + 3b
U5 = U4 + b = (a + 3b) + b = a + 4b
Berdasarkan pola tersebut, dapatkah sobat menentukan suku ke-7, suku ke-26 hingga suku ke-90? Dengan menggunakan pola diatas kita dapat mengetahui dengan mudah suku-suku tersebut.
U7 = a + 6b
U26 = a + 25b
U90 = a + 89b
Sehingga berdasarkan runtutan penjelasan diatas untuk suku ke-n dapat kita peroleh menggunakan rumus :
Un = a + (n – 1)b, untuk n bilangan asli
DERET ARITMATIKA
Yang dimaksud dengan deret aritmatika adalah penjumlahan dari semua anggota barisan aritmatika secara berurutan. Contoh dari deret aritmatika yaitu 7 + 10 + 13 + 16 + 19 + …
Misalnya kita ambil n suku pertama, jika kita ingin menentukan hasil dari deret aritmatika sebagai contoh untuk 5 suku pertama dari contoh deret diatas. Bagaimana caranya?
7 + 10 + 13 + 16 + 19 = 65
Nah untuk 5 suku pertama, masih mungkin kita menghitung manual seperti diatas. Seandainya kita akan menentukan jumlah dari 100 suku pertama, apakah masih mungkin kita menghitung manual seperti itu. Walaupun bisa tetapi pastinya akan memakan waktu yang cukup lama. Nah kali ini akan kita tunjukkan cara menentukannya, sebagai contohnya untuk mennetukan jumlah 5 suku pertama dari contoh diatas.
Misalkan S5=7 + 10 + 13 + 16 + 19, sehingga
Deret Aritmetika
Walaupun dengan cara yang berbeda tetapi menunjukkan hasil yang sama yaitu 65. Perhatikan bahwa S5 tersebut dapat dicari dengan mengalikan hasil penjumlahan suku pertama dan suku ke-5, dengan banyaknya suku pada barisan, kemudian dibagi dengan 2. Analogi dengan hasil ini, jumlah n suku pertama dari suatu barisan dapat dicari dengan rumus berikut:
Sn = (a + Un) × n : 2
Dikarenakan Un = a + (n – 1)b, sehingga rumus di atas menjadi
Sn = (2a + (n – 1)b) × n : 2
DERET ARITMATIKA
Sisipan pada deret aritmatika yaitu menambahkan beberapa buah bilangan diantara dua suku yang berurutan pada suatu deret aritmatika sehingga diperoleh deret aritmatika yang baru. Sebagai contoh :
Deret mula-mula = 4 + 13 + 22 + 31 +……
Setelah disisipi = 4 + 7 + 10 + 13 + 16 + 19 + 22 + 25 + 28 + 31 +……
Untuk beda dari deret baru ini biasanya dinyatakan dengan b1, dapat ditentukan dengan rumus berikut :
b1 = b/(k+1)
b1 = beda deret baru
b = beda deret mula-mula
k = banyak bilangan yang disisipkan
Barisan dan Deret Aritmatika tergolong materi yang mudah dipahami, sehingga diharapkan hanya dengan membaca artikel ini sobat semua telah mengerti tentang materi ini. Walaupun demikian, latihan soal harus tetap berjalan agar kemampuan kita selalu terasah. Materi sebelumnya yang dapat dipelajari juga yaitu Frekuensi Harapan dan Peluang Komplemen Suatu Kejadian dari sub bab peluang.
Selasa, 01 Oktober 2013
TRIGONOMETRI
RUMUS TRIGONOMETRI
Ini dia, rumus-rumus trigonometri yang sering anda pergunakan dalam pembelajaran. Mulai dari rumus dasar hingga nilai max dan min suatu fungsi yang menggunakan trigonometri.
A. Bentuk Umum
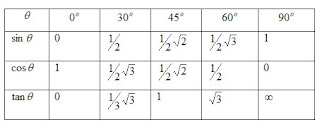
C. Hubungan Sudut Berelasi antara Sin, Cos dan Tangen
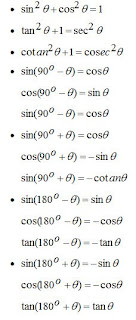
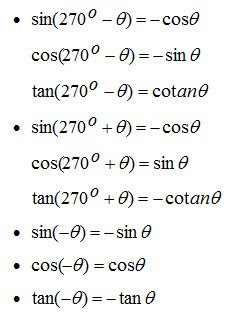
D. Rumus-rumus Trigonometri
1. Aturan sinus
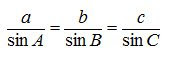
2. Aturan Cosinus
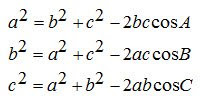
3. Luas Segitiga ABC
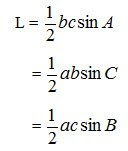
4. Jumlah dan Selish Dua Sudut
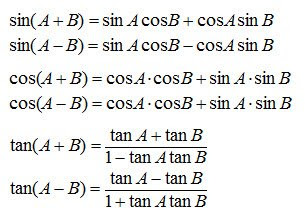
5. Sudut 2A (Sudut Kembar)
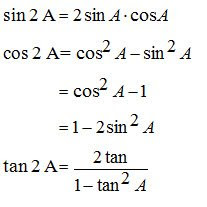
6. Hasil Kali Dua Fungsi Trigonometri
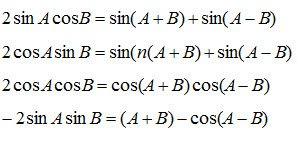
7. Jumlah Selisih Dua Fungsi Trigonometri
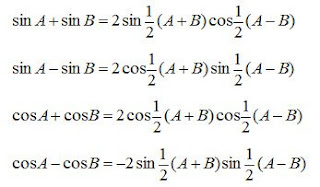
8. Persamaan Trigonometri
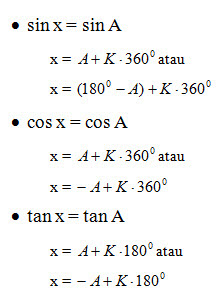
9. Bentuk a Cos x + b Sin x
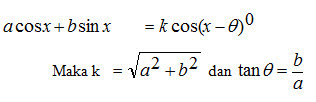
10. Bentuk a Cos x + b Sin x = c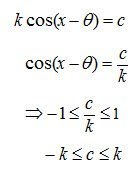
11. Nilai Maksimum dan Minimum Fungsi f(x) =a Cos x + b Sin x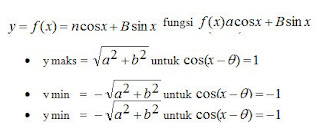
Ini dia, rumus-rumus trigonometri yang sering anda pergunakan dalam pembelajaran. Mulai dari rumus dasar hingga nilai max dan min suatu fungsi yang menggunakan trigonometri.
A. Bentuk Umum

C. Hubungan Sudut Berelasi antara Sin, Cos dan Tangen
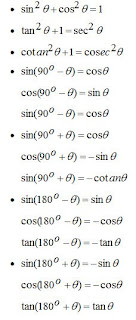
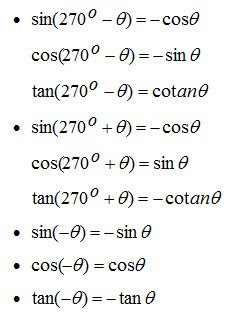
D. Rumus-rumus Trigonometri
1. Aturan sinus
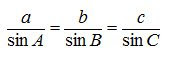
2. Aturan Cosinus
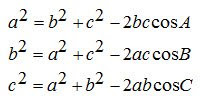
3. Luas Segitiga ABC
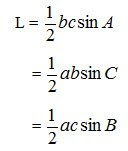
4. Jumlah dan Selish Dua Sudut
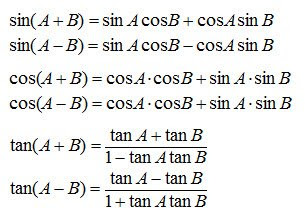
5. Sudut 2A (Sudut Kembar)
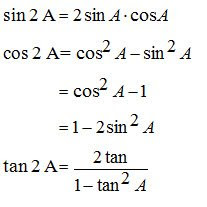
6. Hasil Kali Dua Fungsi Trigonometri
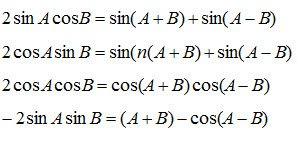
7. Jumlah Selisih Dua Fungsi Trigonometri
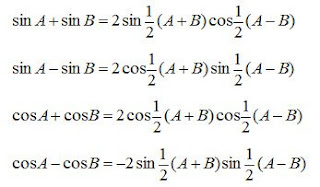
8. Persamaan Trigonometri
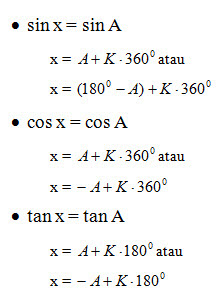
9. Bentuk a Cos x + b Sin x
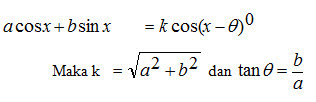
10. Bentuk a Cos x + b Sin x = c
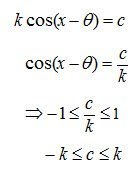
11. Nilai Maksimum dan Minimum Fungsi f(x) =a Cos x + b Sin x
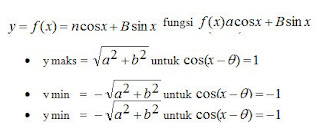
Sabtu, 28 September 2013
kesebangunan
Rumus Kesebangunan
Rumus-rumus kesebangunan sangat dibutuhkan dalam geometri, baik bidang datar maupun bangun ruang. Rumus kesebangunan ini juga mendasari ilmu trigonometri. Dengan demikian sangat penting bagi kita untuk mengingat rumus kesebangunan ini. Berikut ini aalah rumus-rumus kesebangunanDua bangun dikatakan sebangun jika
a. panjang sisi-sisi yang bersesuaian dari kedua bangun tersebut memiliki perbandingan senilai
b. sudut-sudut yang bersesuaian dari kedua bangun tersebut sama besar.
2. Bangun-bangun yang memiliki bentuk dan ukuran yang sama dikatakan bangun-bangun yang kongruen.
3. Syarat dua segitiga sebangun adalah sisi-sisi yang bersesuaian sebanding atau sudut-sudut yang bersesuaian sama besar.
4. Syarat dua segitiga kongruen:
a. Sisi-sisi yang bersesuaian sama panjang (s.s.s)
b. Dua sisi yang bersesuaian sama panjang dan sudut yang diapitnya sama besar (s.sd.s)
c. Dua sudut yang bersesuaian sama besar dan sisi yang berada di antaranya sama panjang (sd.s.sd)
d. Dua sudut yang bersesuaian sama besar dan sisi yang berada di hadapannya sama panjang (sd.sd.s).
Yang pertama : untuk kasus siku-siku
Yang kedua : untuk segitiga sembarang
Penurunan rumus kesebangunan
Berapa panjang PQ jika AB (sisi yang panjang) dan DC (sisi yang pendek) diketahui panjangnya dan perbandingan AP : AC = BQ : BD diketahui.
Jawabannya ADA, simaklah ulasan berikut ini! Langsung aja ke TKP. hehehe
Pada posting sebelumnya, House of Math sudah mengulas cara menyelesaikan soal tersebut. Namun cara yang digunakan lumayan panjang. Nah sekarang House of Math akan mengulas tentang rumus cepat untuk menyelesaikan soal tersebut.
Dengan menggunakan proses berfikir pada posting pembahasan soal tersebut, kita bisa menurunkan rumus cepatnya. Inilah caranya:
1. Kita buat perpanjangan garis PQ di R
2. Misal = AP : AC = BQ : BD = m : n
3. Selanjutnya Pandang segitiga ADC
Berlaku hubungan:
4. Pandang segitiga ABD
Berlaku hubungan:
5. RQ merupakan sebuah garis yang dapat dibentuk olah garis RP dan garis RQ sehingga:
6. Sehingga untuk menghitung panjang PQ dapat langsung menggunakan rumus :
Dengan:
AB = sisi yang panjang
DC = sisi yang pendek
m : n = perbandingan letak P dan Q (kecil : besar)
Sekian penurunan rumus cepatnya, sepanjang itu menghasilkan rumus yang singkat,yang cepat, yang memudahkan pengerjaan soal.
Diposkan oleh farizrizriz di 02:48 Rumus Kesebangunan Matematika
Diposkan oleh Arya Jr di 04.09 Tidak ada komentar:
Kirimkan Ini lewat Email
BlogThis!
Berbagi ke Twitter
Berbagi ke Facebook
Peluang
Peluang, Permutasi & Kombinasi Matematika
Rumus Web mengumpulkan materi Peluang, Permutasi & Kombinasi Matematika ini untuk anak SMA demi UAN SNMPTN SPMB SIMAK UI. Silakan dipelajari :)
1) Permutasi
Permutasi adalah susunan unsur-unsur yang berbeda dalam urutan tertentu. Pada permutasi urutan diperhatikan sehingga
Permutasi k unsur dari n unsur adalah semua urutan yang berbeda yang mungkin dari k unsur yang diambil dari n unsur yang berbeda. Banyak permutasi k unsur dari n unsur ditulis atau .
Permutasi siklis (melingkar) dari n unsur adalah (n-1) !
Cara cepat mengerjakan soal permutasi
dengan penulisan nPk, hitung 10P4
kita langsung tulis 4 angka dari 10 mundur, yaitu 10.9.8.7
jadi 10P4 = 10x9x8x7 berapa itu? hitung sendiri :)
Contoh permutasi siklis :
Suatu keluarga yang terdiri atas 6 orang duduk mengelilingi sebuah meja makan yang berbentuk lingkaran. Berapa banyak cara agar mereka dapat duduk mengelilingi meja makan dengan cara yang berbeda?
Jawab :
Banyaknya cara agar 6 orang dapat duduk mengelilingi meja makan dengan urutan yang berbeda sama dengan banyak permutasi siklis (melingkar) 6 unsur yaitu :
2) Kombinasi
Kombinasi adalah susunan unsur-unsur dengan tidak memperhatikan urutannya. Pada kombinasi AB = BA. Dari suatu himpunan dengan n unsur dapat disusun himpunan bagiannya dengan untuk Setiap himpunan bagian dengan k unsur dari himpunan dengan unsur n disebut kombinasi k unsur dari n yang dilambangkan dengan ,
Contoh :
Diketahui himpunan .
Tentukan banyak himpunan bagian dari himpunan A yang memiliki 2 unsur!
Jawab :
Banyak himpunan bagian dari A yang memiliki 2 unsur adalah C (6, 2).
Cara cepat mengerjakan soal kombinasi
dengan penulisan nCk, hitung 10C4
kita langsung tulis 4 angka dari 10 mundur lalu dibagi 4!, yaitu 10.9.8.7 dibagi 4.3.2.1
jadi 10C4 = 10x9x8x7 / 4x3x2x1 berapa itu? hitung sendiri :)
Ohya jika ditanya 10C6 maka sama dengan 10C4, ingat 10C6=10C4. contoh lainnya
20C5=20C15
3C2=3C1
100C97=100C3
melihat polanya? hehe semoga bermanfaat!
Peluang Matematika
1. Pengertian Ruang Sampel dan Kejadian
Himpunan S dari semua kejadian atau peristiwa yang mungkin mucul dari suatu percobaan disebut ruang sampel. Kejadian khusus atau suatu unsur dari S disebut titik sampel atau sampel. Suatu kejadian A adalah suatu himpunan bagian dari ruang sampel S.
Contoh:
Diberikan percobaan pelemparan 3 mata uang logam sekaligus 1 kali, yang masing-masing memiliki sisi angka ( A ) dan gambar ( G ). Jika P adalah kejadian muncul dua angka, tentukan S, P (kejadian)!
Jawab :
S = { AAA, AAG, AGA, GAA, GAG, AGG, GGA, GGG}
P = {AAG, AGA, GAA}
2. Pengertian Peluang Suatu Kejadian
Pada suatu percobaan terdapat n hasil yang mungkin dan masing-masing berkesempatan sama untuk muncul. Jika dari hasil percobaan ini terdapat k hasil yang merupakan kejadian A, maka peluang kejadian A ditulis P ( A ) ditentukan dengan rumus :
Contoh :
Pada percobaan pelemparan sebuah dadu, tentukanlah peluang percobaan kejadian muncul bilangan genap!
Jawab : S = { 1, 2, 3, 4, 5, 6} maka n ( S ) = 6
Misalkan A adalah kejadian muncul bilangan genap, maka:
A = {2, 4, 6} dan n ( A ) = 3
3. Kisaran Nilai Peluang Matematika
Misalkan A adalah sebarang kejadian pada ruang sampel S dengan n ( S ) = n, n ( A ) = k dan
Jadi, peluang suatu kejadian terletak pada interval tertutup [0,1]. Suatu kejadian yang peluangnya nol dinamakan kejadian mustahil dan kejadian yang peluangnya 1 dinamakan kejadian pasti.
4. Frekuensi Harapan Suatu Kejadian
Jika A adalah suatu kejadian pada frekuensi ruang sampel S dengan peluang P ( A ), maka frekuensi harapan kejadian A dari n kali percobaan adalah n x P( A ).
Contoh :
Bila sebuah dadu dilempar 720 kali, berapakah frekuensi harapan dari munculnya mata dadu 1? Jawab :
Pada pelemparan dadu 1 kali, S = { 1, 2, 3, 4, 5, 6 } maka n (S) = 6.
Misalkan A adalah kejadian munculnya mata dadu 1, maka:
A = { 1 } dan n ( A ) sehingga :
Frekuensi harapan munculnya mata dadu 1 adalah
5. Peluang Komplemen Suatu Kejadian
Misalkan S adalah ruang sampel dengan n ( S ) = n, A adalah kejadian pada ruang sampel S, dengan n ( A ) = k dan Ac adalah komplemen kejadian A, maka nilai n (Ac) = n – k, sehingga :
Jadi, jika peluang hasil dari suatu percobaan adalah P, maka peluang hasil itu tidak terjadi adalah (1 – P).
Peluang Kejadian Majemuk
1. Gabungan Dua Kejadian
Untuk setiap kejadian A dan B berlaku :
Catatan : dibaca “ Kejadian A atau B dan dibaca “Kejadian A dan B”
Contoh :
Pada pelemparan sebuah dadu, A adalah kejadian munculnya bilangan komposit dan B adalah kejadian muncul bilangan genap. Carilah peluang kejadian A atau B!
Jawab :
2. Kejadian-kejadian Saling Lepas
Untuk setiap kejadian berlaku Jika . Sehingga Dalam kasus ini, A dan B disebut dua kejadian saling lepas.
3. Kejadian Bersyarat
Jika P (B) adalah peluang kejadian B, maka P (A|B) didefinisikan sebagai peluang kejadian A dengan syarat B telah terjadi. Jika adalah peluang terjadinya A dan B, maka Dalam kasus ini, dua kejadian tersebut tidak saling bebas.
4. Teorema Bayes
Teorema Bayes(1720 – 1763) mengemukakan hubungan antara P (A|B) dengan P ( B|A ) dalam teorema berikut ini :
5. Kejadian saling bebas Stokhastik
(i) Misalkan A dan B adalah kejadian – kejadian pada ruang sampel S, A dan B disebut dua kejadian saling bebas stokhastik apabila kemunculan salah satu tidak dipengaruhi kemunculan yang lainnya atau : P (A | B) = P (A), sehingga:
Sebaran Peluang
1. Pengertian Peubah acak dan Sebaran Peluang.
Peubah acak X adalah fungsi dari suatu sampel S ke bilangan real R. Jika X adalah peubah acak pada ruang sampel S denga X (S) merupakan himpunan berhingga, peubah acak X dinamakan peubah acak diskrit. Jika Y adalah peubah acak pada ruang sampel S dengan Y(S) merupakan interval, peubah acak Y disebut peubah acak kontinu. Jika X adalah fungsi dari sampel S ke himpunan bilangan real R, untuk setiap dan setiap maka:
Misalkan X adalah peubah acak diskrit pada ruang sampel S, fungsi masa peluang disingkat sebaran peluang dari X adalah fungsi f dari R yang ditentukan dengan rumus berikut :
2. Sebaran Binom
Sebaran Binom atau Distribusi Binomial dinyatakan dengan rumus sebagai berikut :
Dengan P sebagai parameter dan
Rumus ini dinyatakan sebagai:
untuk n = 0, 1, 2, …. ,n
Dengan P sebagai parameter dan
P = Peluang sukses
n = Banyak percobaan
x = Muncul sukses
n-x = Muncul gagalRumus Peluang









