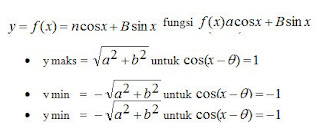Selasa, 15 Oktober 2013
Sabtu, 05 Oktober 2013
Persamaan Linier Satu Variabel (PLSV)
Persamaan Linier Satu Variabel (PLSV)
Persamaan linier satu variable adalah persamaan yang hanya menggunakan satu variable saja (hanya satu variable)
1. Kalimat terbuka
Kalimat terbuka adalah kalimat matematika yang belum jelas benar dan salahnya.
Kalimat pernyataan adalah kalimat yang mempunyai nilai benar atau salah
Contoh kalimat benar
Jumlah dari enam dan dua adalah delapan
Enam dikurangi dua adalah empat
Contoh kalimat salah
Tujuh habis dibagi tiga
Persegi memiliki satu sisi
Jadi
Kalimat benar adalah kalimat yang pernyataannya memiliki nilai benar
Kalimat salah adalah kalimat yang pernyataannya memiliki nilai salah
2. Persamaan linier Satu Variabel
Pesamaan linier satu variable adalah persamaan yang hanya menggunakan satu variable saja (hanya satu variable)
Bentuk umum
ax + b = c 0, x = perubah
Persamaan linier dapat diselesaikan dengan cara
a. Menambah, mengurangi, membagi atau mengali dengan bilangan yang sama
b. Setiap pemindahan ruas, dari kirikekanan atau sebaliknya dapat diikuti perubahan tanda dari positif ke negatif atau sebaliknya.
Contoh
1. 4x -12 = 20
Jawab
4x -12 = 20
4x = 20 + 12
4x = 32
x= 8
2. 5x -20 = 10
Jawab
5x – 20 = 10
5x = 20 + 10
5x = 30
x = 6
Penerapan Untuk Persamaan Linier dalam Sehari-hari
Contoh
Jumlah siswa kelas 2 adalah 40 siswa. Jika jumlah siswa laki-laki sebanyak 12 siswa, berapa jumlah siswa perempuan.
Jawab
a + 12 = 40
a = 40 -12
a = 28
Persamaan linier satu variable adalah persamaan yang hanya menggunakan satu variable saja (hanya satu variable)
1. Kalimat terbuka
Kalimat terbuka adalah kalimat matematika yang belum jelas benar dan salahnya.
Kalimat pernyataan adalah kalimat yang mempunyai nilai benar atau salah
Contoh kalimat benar
Jumlah dari enam dan dua adalah delapan
Enam dikurangi dua adalah empat
Contoh kalimat salah
Tujuh habis dibagi tiga
Persegi memiliki satu sisi
Jadi
Kalimat benar adalah kalimat yang pernyataannya memiliki nilai benar
Kalimat salah adalah kalimat yang pernyataannya memiliki nilai salah
2. Persamaan linier Satu Variabel
Pesamaan linier satu variable adalah persamaan yang hanya menggunakan satu variable saja (hanya satu variable)
Bentuk umum
ax + b = c 0, x = perubah
Persamaan linier dapat diselesaikan dengan cara
a. Menambah, mengurangi, membagi atau mengali dengan bilangan yang sama
b. Setiap pemindahan ruas, dari kirikekanan atau sebaliknya dapat diikuti perubahan tanda dari positif ke negatif atau sebaliknya.
Contoh
1. 4x -12 = 20
Jawab
4x -12 = 20
4x = 20 + 12
4x = 32
x= 8
2. 5x -20 = 10
Jawab
5x – 20 = 10
5x = 20 + 10
5x = 30
x = 6
Penerapan Untuk Persamaan Linier dalam Sehari-hari
Contoh
Jumlah siswa kelas 2 adalah 40 siswa. Jika jumlah siswa laki-laki sebanyak 12 siswa, berapa jumlah siswa perempuan.
Jawab
a + 12 = 40
a = 40 -12
a = 28
Barisan dan Deret Aritmatika
BARISAN ARITMATIKA
Barisan bilangan adalah urutan dari bilangan yang dibuat berdasarkan aturan tertentu. Sedangkan untuk barisan aritmatika adalah sebuah barisan bilangan dimana setiap pasangan suku-suku yang berurutan memiliki selisih yang sama. contoh : 4,6,8,10,....
Selisih bilangan pada barisan aritmatika disebut beda yang biasa disimbolkan dengan huruf b, untuk contoh diatas memiliki nilai beda 2. Dan bilangan yang menyusun suatu barisan disebut suku, dimana suku ke n dari suatu barisan disimbolkan dengan Un sehingga untuk suku ke 5 dari suatu barisan biasa disebut dengan U5. Khusus untuk suku pertama dari suatu barisan biasa disimbolkan dengan huruf a.
Jadi bentuk umum untuk suatu barisan aritmatika yaitu U1,U2,U3, … ,Un-1 atau a, a+b, a+2b, … , a+(n-1)b
Menentukan Rumus Suku ke-n suatu barisan
Pasangan suku-suku berurutan dari suatu barisan aritmatika mempunyai beda yang sama, maka
U2 = a + b
U3 = U2 + b = (a + b) + b = a + 2b
U4 = U3 + b = (a + 2b) + b = a + 3b
U5 = U4 + b = (a + 3b) + b = a + 4b
Berdasarkan pola tersebut, dapatkah sobat menentukan suku ke-7, suku ke-26 hingga suku ke-90? Dengan menggunakan pola diatas kita dapat mengetahui dengan mudah suku-suku tersebut.
U7 = a + 6b
U26 = a + 25b
U90 = a + 89b
Sehingga berdasarkan runtutan penjelasan diatas untuk suku ke-n dapat kita peroleh menggunakan rumus :
Un = a + (n – 1)b, untuk n bilangan asli
DERET ARITMATIKA
Yang dimaksud dengan deret aritmatika adalah penjumlahan dari semua anggota barisan aritmatika secara berurutan. Contoh dari deret aritmatika yaitu 7 + 10 + 13 + 16 + 19 + …
Misalnya kita ambil n suku pertama, jika kita ingin menentukan hasil dari deret aritmatika sebagai contoh untuk 5 suku pertama dari contoh deret diatas. Bagaimana caranya?
7 + 10 + 13 + 16 + 19 = 65
Nah untuk 5 suku pertama, masih mungkin kita menghitung manual seperti diatas. Seandainya kita akan menentukan jumlah dari 100 suku pertama, apakah masih mungkin kita menghitung manual seperti itu. Walaupun bisa tetapi pastinya akan memakan waktu yang cukup lama. Nah kali ini akan kita tunjukkan cara menentukannya, sebagai contohnya untuk mennetukan jumlah 5 suku pertama dari contoh diatas.
Misalkan S5=7 + 10 + 13 + 16 + 19, sehingga
Deret Aritmetika
Walaupun dengan cara yang berbeda tetapi menunjukkan hasil yang sama yaitu 65. Perhatikan bahwa S5 tersebut dapat dicari dengan mengalikan hasil penjumlahan suku pertama dan suku ke-5, dengan banyaknya suku pada barisan, kemudian dibagi dengan 2. Analogi dengan hasil ini, jumlah n suku pertama dari suatu barisan dapat dicari dengan rumus berikut:
Sn = (a + Un) × n : 2
Dikarenakan Un = a + (n – 1)b, sehingga rumus di atas menjadi
Sn = (2a + (n – 1)b) × n : 2
DERET ARITMATIKA
Sisipan pada deret aritmatika yaitu menambahkan beberapa buah bilangan diantara dua suku yang berurutan pada suatu deret aritmatika sehingga diperoleh deret aritmatika yang baru. Sebagai contoh :
Deret mula-mula = 4 + 13 + 22 + 31 +……
Setelah disisipi = 4 + 7 + 10 + 13 + 16 + 19 + 22 + 25 + 28 + 31 +……
Untuk beda dari deret baru ini biasanya dinyatakan dengan b1, dapat ditentukan dengan rumus berikut :
b1 = b/(k+1)
b1 = beda deret baru
b = beda deret mula-mula
k = banyak bilangan yang disisipkan
Barisan dan Deret Aritmatika tergolong materi yang mudah dipahami, sehingga diharapkan hanya dengan membaca artikel ini sobat semua telah mengerti tentang materi ini. Walaupun demikian, latihan soal harus tetap berjalan agar kemampuan kita selalu terasah. Materi sebelumnya yang dapat dipelajari juga yaitu Frekuensi Harapan dan Peluang Komplemen Suatu Kejadian dari sub bab peluang.
Barisan bilangan adalah urutan dari bilangan yang dibuat berdasarkan aturan tertentu. Sedangkan untuk barisan aritmatika adalah sebuah barisan bilangan dimana setiap pasangan suku-suku yang berurutan memiliki selisih yang sama. contoh : 4,6,8,10,....
Selisih bilangan pada barisan aritmatika disebut beda yang biasa disimbolkan dengan huruf b, untuk contoh diatas memiliki nilai beda 2. Dan bilangan yang menyusun suatu barisan disebut suku, dimana suku ke n dari suatu barisan disimbolkan dengan Un sehingga untuk suku ke 5 dari suatu barisan biasa disebut dengan U5. Khusus untuk suku pertama dari suatu barisan biasa disimbolkan dengan huruf a.
Jadi bentuk umum untuk suatu barisan aritmatika yaitu U1,U2,U3, … ,Un-1 atau a, a+b, a+2b, … , a+(n-1)b
Menentukan Rumus Suku ke-n suatu barisan
Pasangan suku-suku berurutan dari suatu barisan aritmatika mempunyai beda yang sama, maka
U2 = a + b
U3 = U2 + b = (a + b) + b = a + 2b
U4 = U3 + b = (a + 2b) + b = a + 3b
U5 = U4 + b = (a + 3b) + b = a + 4b
Berdasarkan pola tersebut, dapatkah sobat menentukan suku ke-7, suku ke-26 hingga suku ke-90? Dengan menggunakan pola diatas kita dapat mengetahui dengan mudah suku-suku tersebut.
U7 = a + 6b
U26 = a + 25b
U90 = a + 89b
Sehingga berdasarkan runtutan penjelasan diatas untuk suku ke-n dapat kita peroleh menggunakan rumus :
Un = a + (n – 1)b, untuk n bilangan asli
DERET ARITMATIKA
Yang dimaksud dengan deret aritmatika adalah penjumlahan dari semua anggota barisan aritmatika secara berurutan. Contoh dari deret aritmatika yaitu 7 + 10 + 13 + 16 + 19 + …
Misalnya kita ambil n suku pertama, jika kita ingin menentukan hasil dari deret aritmatika sebagai contoh untuk 5 suku pertama dari contoh deret diatas. Bagaimana caranya?
7 + 10 + 13 + 16 + 19 = 65
Nah untuk 5 suku pertama, masih mungkin kita menghitung manual seperti diatas. Seandainya kita akan menentukan jumlah dari 100 suku pertama, apakah masih mungkin kita menghitung manual seperti itu. Walaupun bisa tetapi pastinya akan memakan waktu yang cukup lama. Nah kali ini akan kita tunjukkan cara menentukannya, sebagai contohnya untuk mennetukan jumlah 5 suku pertama dari contoh diatas.
Misalkan S5=7 + 10 + 13 + 16 + 19, sehingga
Deret Aritmetika
Walaupun dengan cara yang berbeda tetapi menunjukkan hasil yang sama yaitu 65. Perhatikan bahwa S5 tersebut dapat dicari dengan mengalikan hasil penjumlahan suku pertama dan suku ke-5, dengan banyaknya suku pada barisan, kemudian dibagi dengan 2. Analogi dengan hasil ini, jumlah n suku pertama dari suatu barisan dapat dicari dengan rumus berikut:
Sn = (a + Un) × n : 2
Dikarenakan Un = a + (n – 1)b, sehingga rumus di atas menjadi
Sn = (2a + (n – 1)b) × n : 2
DERET ARITMATIKA
Sisipan pada deret aritmatika yaitu menambahkan beberapa buah bilangan diantara dua suku yang berurutan pada suatu deret aritmatika sehingga diperoleh deret aritmatika yang baru. Sebagai contoh :
Deret mula-mula = 4 + 13 + 22 + 31 +……
Setelah disisipi = 4 + 7 + 10 + 13 + 16 + 19 + 22 + 25 + 28 + 31 +……
Untuk beda dari deret baru ini biasanya dinyatakan dengan b1, dapat ditentukan dengan rumus berikut :
b1 = b/(k+1)
b1 = beda deret baru
b = beda deret mula-mula
k = banyak bilangan yang disisipkan
Barisan dan Deret Aritmatika tergolong materi yang mudah dipahami, sehingga diharapkan hanya dengan membaca artikel ini sobat semua telah mengerti tentang materi ini. Walaupun demikian, latihan soal harus tetap berjalan agar kemampuan kita selalu terasah. Materi sebelumnya yang dapat dipelajari juga yaitu Frekuensi Harapan dan Peluang Komplemen Suatu Kejadian dari sub bab peluang.
Selasa, 01 Oktober 2013
TRIGONOMETRI
RUMUS TRIGONOMETRI
Ini dia, rumus-rumus trigonometri yang sering anda pergunakan dalam pembelajaran. Mulai dari rumus dasar hingga nilai max dan min suatu fungsi yang menggunakan trigonometri.
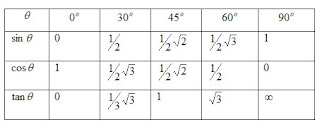
A. Bentuk Umum
C. Hubungan Sudut Berelasi antara Sin, Cos dan Tangen
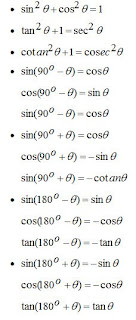
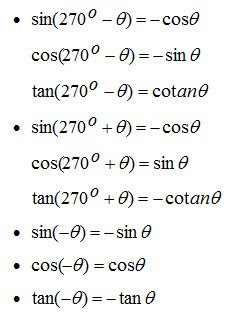
D. Rumus-rumus Trigonometri
1. Aturan sinus
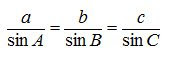
2. Aturan Cosinus
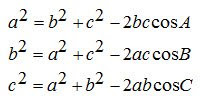
3. Luas Segitiga ABC
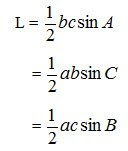
4. Jumlah dan Selish Dua Sudut
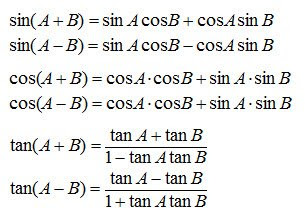
5. Sudut 2A (Sudut Kembar)
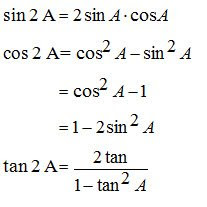
6. Hasil Kali Dua Fungsi Trigonometri
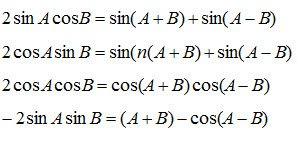
7. Jumlah Selisih Dua Fungsi Trigonometri
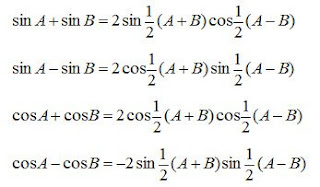
8. Persamaan Trigonometri
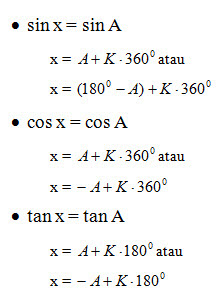
9. Bentuk a Cos x + b Sin x
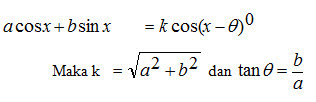
10. Bentuk a Cos x + b Sin x = c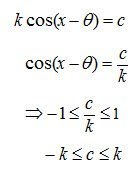
11. Nilai Maksimum dan Minimum Fungsi f(x) =a Cos x + b Sin x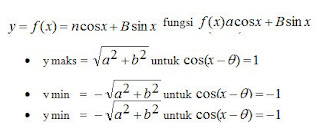
Ini dia, rumus-rumus trigonometri yang sering anda pergunakan dalam pembelajaran. Mulai dari rumus dasar hingga nilai max dan min suatu fungsi yang menggunakan trigonometri.
A. Bentuk Umum

C. Hubungan Sudut Berelasi antara Sin, Cos dan Tangen
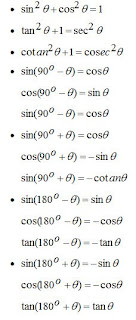
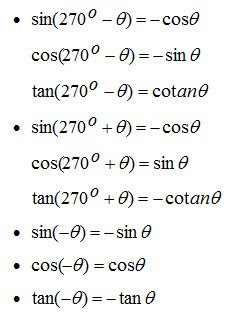
D. Rumus-rumus Trigonometri
1. Aturan sinus
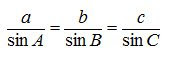
2. Aturan Cosinus
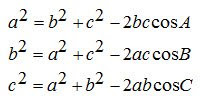
3. Luas Segitiga ABC
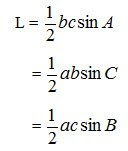
4. Jumlah dan Selish Dua Sudut
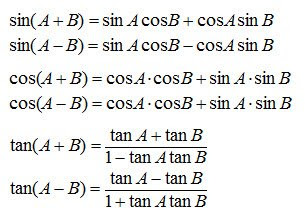
5. Sudut 2A (Sudut Kembar)
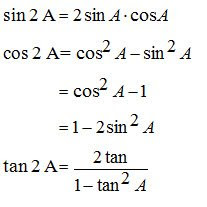
6. Hasil Kali Dua Fungsi Trigonometri
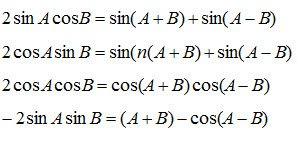
7. Jumlah Selisih Dua Fungsi Trigonometri
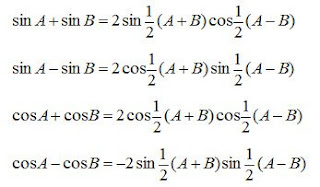
8. Persamaan Trigonometri
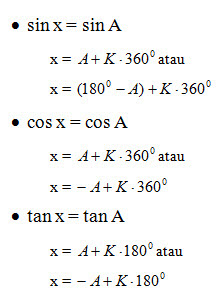
9. Bentuk a Cos x + b Sin x
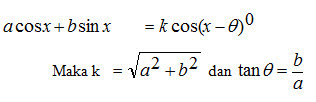
10. Bentuk a Cos x + b Sin x = c
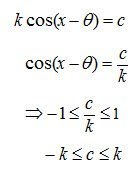
11. Nilai Maksimum dan Minimum Fungsi f(x) =a Cos x + b Sin x